虽然DQN的表现很好,但它有一个致命的缺点是无法学习连续动作空间。回想一下,DQN 是根据greddy策略找到最大Q值对应的行为,即 \(\large a = \mathop{argmax}\limits_{a \in \mathcal{A}} Q(s)\),也就说每一个行为对应一个Q值,当动作是高维度的或者是连续的,那么DQN的计算代价就很大,甚至无法进行学习。这时使用策略梯度就能很好解决这个问题。我们把环境动作设计成连续的,用动作特征表示一个动作,使用策略梯度,我们不需要计算每一个动作的Q值,而是可以通过参数化近似的办法直接输出一个动作特征,而不是从某个值映射到某个动作。DDPG (Deep Deterministic Policy Gradient)算法很好的弥补了DQN的缺陷。当然,并不是DDPG只能解决连续动作问题,只要把动作特征映射到某一个动作上就能应对非连续动作空间问题了。
算法
DDPG使用演员-评论家模型(actor-critic),设计了4个参数化函数。其中actor包含策略函数 \(\large \mu\),目标策略函数 \(\large \mu'\),而critic包含Q函数 \(\large Q\),目标Q函数 \(\large Q'\)。
我们的目标是把 \(\large \mu\) 参数训练好,因为届时我们获取动作特征的方法是,
\[ a = \mu(s) \]
在训练过程中,critic的 \(\large Q\) 的作用是对actor策略 \(\large \mu\) 进行评估,
\[ \begin{aligned} a &= \mu(s) \\ q &= Q(s, a) \end{aligned} \]
通过 \(\large Q(s, a)\) 可以一个评价当前actor在状态 \(\large s\) 执行动作 \(\large a\) 的分数。
上面提到的参数中,目标参数 \(\large \mu'\) 和 \(\large Q'\) 作为监督者,以此来计算 \(\large \mu\) 和 \(\large Q\) 函数的参数梯度。
每一个episode,我们先从经验池 \(\large R\) 中抽样 \(\large N\) 个转移,
\[ (s_i, a_i, r_i, s_{i+1})_i^N \in R \]
对于 \(\large Q\) 的损失函数,我们定义为:
\[ \begin{aligned} & a_{i+1} = \mu'(s_{i+1}) \\ & y_i = r_i + \gamma Q'(s_{i+1}, a_{i+1}) \\ & J = \frac{1}{N} \sum_i (y_i-Q(s_i,a))^2 \end{aligned} \]
对于 \(\large \mu\) 的损函数,论文中直接给的是梯度公式。而我参考了其他人的实现,发现他们定义了一个相对简单的损失函数。
\[ \begin{aligned} & a_i = \mu(s_i) \\ & J = -\frac{1}{N} \sum_i Q(s_i,a_i) \end{aligned} \]
大概理解就是,我们设法把 \(\large Q(s_i,a_i)\) 最大化,即通过梯度下降,最小化其负数。
更新完梯度后,需要进行参数软更新(soft-update):
\[ \begin{aligned} w^{Q'} &= \tau \; w^{Q} + (1-\tau)w^{Q'} \\ w^{\mu'} &= \tau \; w^{\mu} + (1-\tau)w^{\mu'} \\ \tau &\ll 1 \end{aligned} \]
每次更新target参数时,我们不会完全更新,而是保留多一些过往的记忆。
论文中提到,为了让的动作更加丰富,使个体勇于探索,我们要在动作特征上加入噪音。
\[ \mu(s) = \mu(s) + \epsilon \; \mathcal{N} \]
其中 \(\large \mathcal{N}\) 使用Ornstein-Uhlenbeck process算法生成噪音。其中 \(\large \epsilon\) 是一个动态的衰减系数,论文中没有提到,实际使用时如果不加可能导致训练过程非常震荡。
实验细节
论文后面附加部分提供了算法参数的一些细节。
- 梯度更新使用Adam,actor和critic的学习率分别为1e-4和1e-3。
- \(\gamma\) 为0.99
- \(\large \tau\) 为0.001
- 参数化近似使用神经网络,actor和critic使用三层神经网络,分别是400,300和300个神经元。actor的输出层使用tanh。critic第一层输入状态特征,第一层的输出与动作特征一起输入第二层。
- 参数初始化,前两层使用fanin_init初始化,最后一层使用区间为[-3e-3, 3e-3]的归一化分布。
- Ornstein-Uhlenbeck process的参数中,\(\large \theta\) 为0.15,\(\large \sigma\) 为0.2
还有一个就是噪音衰减的问题,这个问题论文中没有提到,但我自己测试时去发现了这个问题不容忽视。\(\large \epsilon\) 初始值为1,每完成一个episode就减去 \(\large d\),这个 \(\large d\) 的很难选,假设是0.01,那么100个episode后 \(\large \epsilon\) 就衰减到0,之后就无法加入噪音了。如果你的模型训练难度较大,要训练几百上千个episode,你必须确保能够持续加入噪音,同时兼顾到训练后期减少噪音的加入。
代码实现
我用pytorch实现了DDPG算法,详见Github
测试
以下是我自己跑的测试结果,测试过程表明某些参数的调节是非常重要的。
MountainCarContinuous-v0
环境细节看这里,小车到达终点就能获得100的奖励。这个环境中小车很容易就找到前往终点的路,所以噪声的衰减可以大一些,设置 \(\large d=0.01\)。
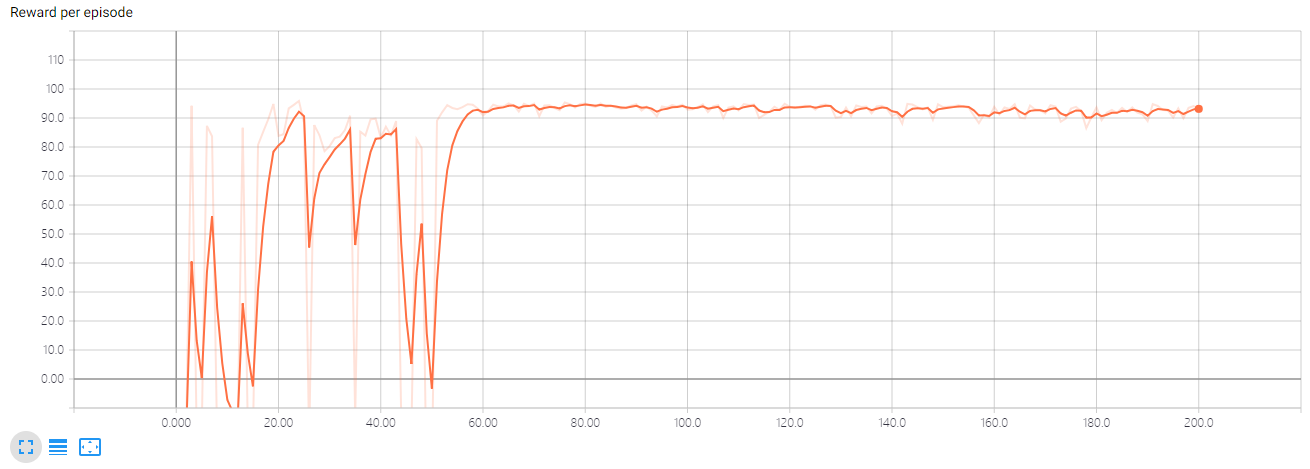
可以看到,小车通过探索很快就找到了终点,并且奖励也接近最优,但因为仍然在往动作中加入噪声,所以小车在尝试有没有更好的路径,经过一番挣扎后,小车发现别的路径都行不通,而此时噪声已经几乎没有了,所以不再进行探索,又回到了之前的获得高奖励的路径上。
如果我们设置 \(\large d=0.001\),表现如下:
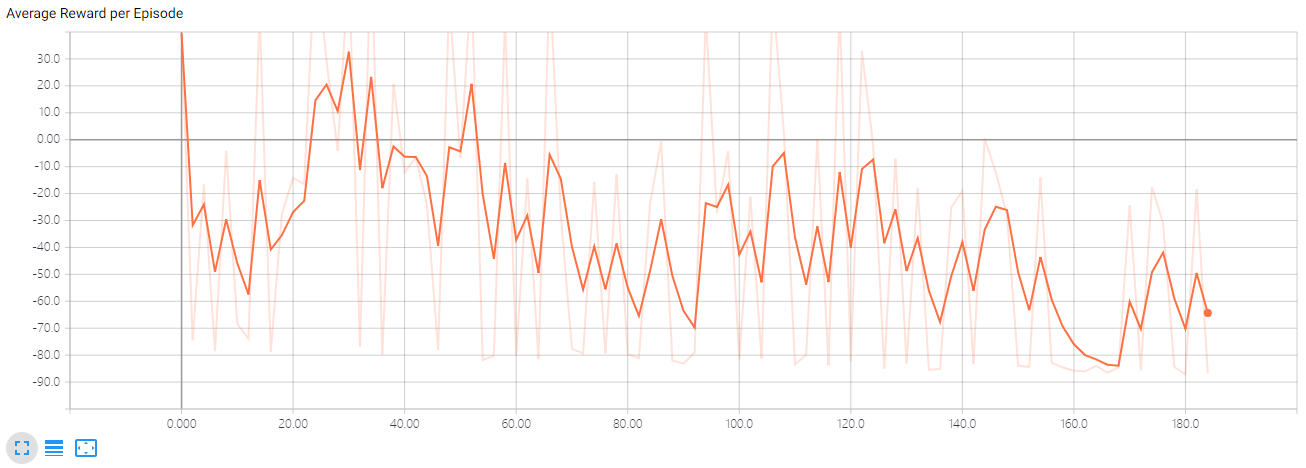
可以发现,噪声衰减调小了,使得小车进行持续的探索。上图经历的episode较少,虽然最终可能找到优秀的路径,但时间代价会很大。原本很快就能解决问题的,没有必要进行长时间的探索。
Pendulum-v0
这个是一个未解决环境,即没有一个奖励区间能说明已经解决。环境细节可以参考这里。
因为环境动作多样化,我们可以进行更多的探索,所以把噪声衰减调节慢一点,设置 \(\large d=0.001\)。
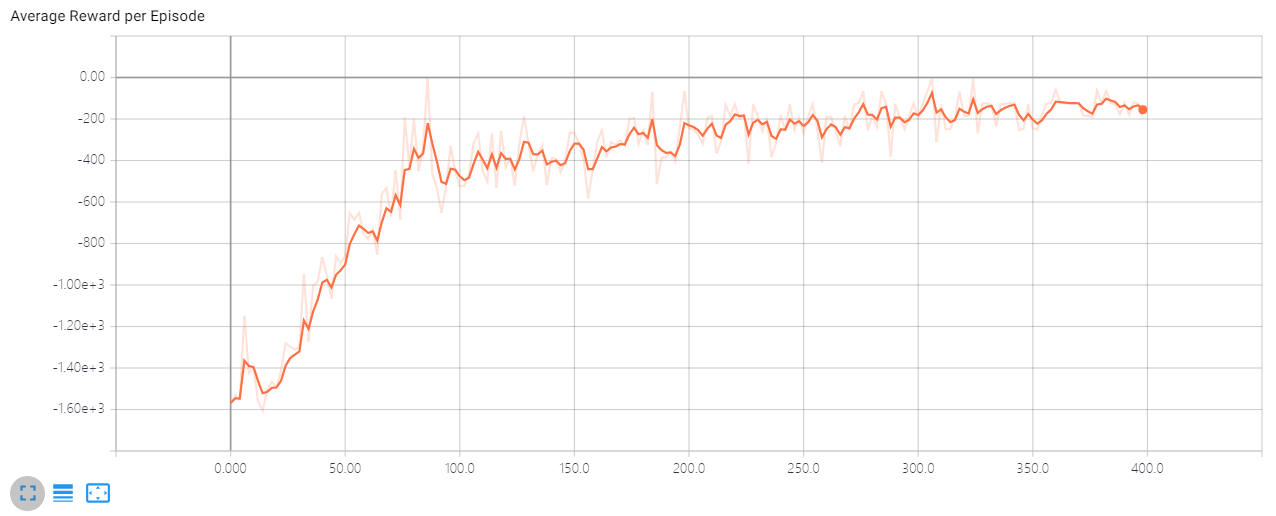
奖励虽然在增长,但一直在负数,后期收敛极慢。而曲线仍然在震荡是因为我们的噪声还没衰减到0。

Comments