以前写的一篇文章,补个档。本文主要推导了一下卷积神经网络的反向传播过程。
卷积层的前向传播
在讲反向传播之前,我先来温习一下卷积层的前向传播。
\[ \begin{pmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{pmatrix} * \begin{pmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} = \begin{pmatrix} z_{11} & z_{12} \\ z_{21} & z_{22} \end{pmatrix} \]
注意,参照维基百科,这里的运算符 \(\large*\) 是卷积的意思,不是乘法。
如果我们展开来写就是这样:
\[ z_{11} = x_{11}w_{11} + x_{12}w_{12} + x_{21}w_{21} + x_{22}w_{22} + b_{11} \] \[ z_{12} = x_{12}w_{11} + x_{13}w_{12} + x_{22}w_{21} + x_{23}w_{22} + b_{12} \] \[ z_{21} = x_{21}w_{11} + x_{22}w_{12} + x_{31}w_{21} + x_{32}w_{22} + b_{21} \] \[ z_{22} = x_{22}w_{11} + x_{23}w_{12} + x_{32}w_{21} + x_{33}w_{22} + b_{22} \]
卷积层的反向传播
以该图两个层卷积层为例
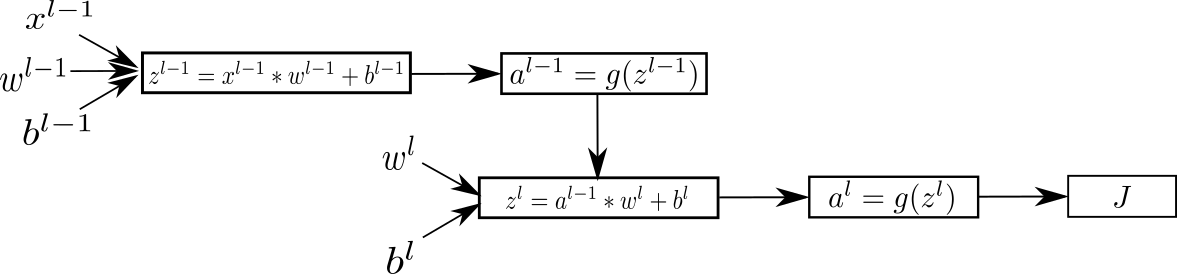
设损失函数为 \(J\) ,第 \(l\) 层的 \(a\) 的梯度值就是
\[ da^l = \frac{d J}{d a^{l}} \]
根据链式法则,\(z^l\) 的梯度值就为
\[ dz^l = \frac{\partial J}{\partial z^{l}} = \frac{d J}{d a^l} \, \frac{da^l}{dz^l} = da^l \, g'(z^l) \]
已经知道 \(z^l\) 后,我们就要去计算梯度值 \(dx^l\), 即上一层的 $da^{l-1} $。但也许你会注意到,上面的卷积操作是一个矩阵操作,但是矩阵要怎么求导呀?这里,我们先不考虑矩阵的求导,我们先尝试对展开式去求导,为了简洁,我们省略参数的 \(l\)。
由上面我们提到的
\[ z_{11} = x_{11}w_{11} + x_{12}w_{12} + x_{21}w_{21} + x_{22}w_{22} + b_{11} \]
以 \(x_{11}\) 为自变量求导得
\[ dx_{11} = \frac{\partial J}{\partial z_{11}} \, \frac{dz_{11}}{dx_{11}} + \frac{\partial J}{\partial z_{12}} \, \frac{dz_{12}}{dx_{11}} + \frac{\partial J}{\partial z_{21}} \, \frac{dz_{21}}{dx_{11}} + \frac{\partial J}{\partial z_{22}} \, \frac{dz_{22}}{dx_{11}} \]
即等于
\[ dx_{11} = dz_{11}w_{11} + 0 + 0 + 0 \]
对于 \(dx_{12}\) ,那么同理
\[ dx_{12} = \frac{\partial J}{\partial z_{11}} \, \frac{dz_{11}}{dx_{12}} + \frac{\partial J}{\partial z_{12}} \, \frac{dz_{12}}{dx_{12}} + \frac{\partial J}{\partial z_{21}} \, \frac{dz_{21}}{dx_{12}} + \frac{\partial J}{\partial z_{22}} \, \frac{dz_{22}}{dx_{12}} \]
\[ dx_{12} = dz_{11}w_{11} + dz_{12}w_{11} + 0 + 0 \]
那么其他 \(x_{ij}\) 同理。都写出来后,就会发现,我们可以写成一个矩阵的卷积操作:
\[ \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & dz_{11} & dz_{12} & 0 \\ 0 & dz_{21} & dz_{22} & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} * \begin{pmatrix} w_{22} & w_{21} \\ w_{12} & w_{11} \end{pmatrix} = \begin{pmatrix} dx_{11} & dx_{12} & dx_{13} \\ dx_{21} & dx_{22} & dx_{23} \\ dx_{31} & dx_{32} & dx_{33} \end{pmatrix} \]
这样的话,我们就可以总结出公式:
\[ dx^{l} = da^{l-1} = pad(dz^{l}) * rot180(W^l) \]
\(pad(dz^{l})\) 表示将 \(dz^l\) 填充 \(0\) 来扩大到合适的维度,\(rot180(W^l)\) 表示将卷积核 \(W^l\) 旋转180度。
那么当我们计算\(dw\)的时候,也可以得出一个卷积公式:
\[ \begin{pmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{pmatrix} * \begin{pmatrix} dz_{11} & dz_{12} \\ dz_{21} & dz_{22} \end{pmatrix} = \begin{pmatrix} dw_{11} & dw_{12} \\ dw_{21} & dw_{22} \end{pmatrix} \]
\[ dw^{l} = \frac{dz^l}{dw^l} = x^l * dz^{l} \]
而偏置项的梯度值 \(db\) 为
\[ db^l = \frac{dz^l}{db^l} = dz^{l} \]
池化层的前向传播
温习一下池化层的前向传播时是怎么算的。
如果是平均池化(AvgPooling), 假设池化层大小是一个 \(2×2\),即每次的池化范围是\(m = 4\),那么每一个池化区域可得
\[ avg(x) = \frac{1}{m} \sum_{k=1}^{m}x_k \]
如果是最大池化(MaxPooling),假设池化层大小是一个 \(2×2\),即每次的池化范围是\(m = 4\),那么每一个池化区域可得
\[ max(x) = max(x_1, x_2, ..., x_m) \]
池化层的反向传播
池化层和激活函数一样,相当于卷积层中的一个子层,没有学习参数,他们会将反向传播得到的梯度值向后传递。

比如说,一个 \(2×2\) 池化层, 即每一个池化区域大小为\(m = 4\),从上一层反向传递过来的是这样一个矩阵
\[ dout = \begin{pmatrix} dx_1 & dx_2 \\ dx_3 & dx_4 \end{pmatrix} \]
当计算梯度值时,需要先将参数还原到输入时的维度
\[ dout = \begin{pmatrix} dx_1 & dx_1 & dx_2 & dx_2 \\ dx_1 & dx_1 & dx_2 & dx_2 \\ dx_3 & dx_3 & dx_4 & dx_4 \\ dx_3 & dx_3 & dx_4 & dx_4 \end{pmatrix} \]
如果是AvgPooling,我们定义\(dout\) 中每一个池化区域的梯度值为 \(davg(x)\) ,该区域中每一个值的导数为
\[ dx_{k} = \frac{d}{dx_{k}}avg(x) = \frac{1}{m} \]
那么整个\(x\) 矩阵往后传递的梯度值为
\[ dx = da^l = \frac{dout}{dx} = \begin{pmatrix} \frac{1}{m} & \frac{1}{m} & \frac{1}{m} & \frac{1}{m} \\ \frac{1}{m} & \frac{1}{m} & \frac{1}{m} & \frac{1}{m} \\ \frac{1}{m} & \frac{1}{m} & \frac{1}{m} & \frac{1}{m} \\ \frac{1}{m} & \frac{1}{m} & \frac{1}{m} & \frac{1}{m} \end{pmatrix} \; dout \]
如果是MaxPooling,我们定义\(dout\) 中每一个池化区域的梯度值为 \(dmax(x)\) ,该区域中每一个值的导数为
\[ dx_{k} = \frac{d}{dx_{k}}max(x) = \begin{cases} 1, & \text{if $x_k$ = max(x)} \\[2ex] 0, & \text{otherwise} \end{cases} \]
那么整个\(x\) 矩阵往后传递的梯度值为
\[ dx = da^l = \frac{dout}{dx} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \end{pmatrix} \; dout \]

Comments