布隆过滤器是一种空间高效的数据结构,用于判断一个元素是否位于集合中,但空间高效是有代价的。它基本实现方式是把元素计算成一个小序列存到数据结构中,多个序列有一定几率会在数据结构中重叠,所以有一定几率会判断错误,而且数据转换成序列后是不可逆的。所以,该数据结构一般用于容错高的场景,作为一个额外的数据结构来判断元素是否在集合中。
基本思路
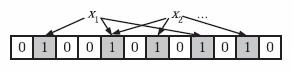
设置一个长度为\(w\)的位数组\(A\),只存0和1,初始都是0。当想插入\(x\)值,先对\(x\)做\(k\)次哈希,得到\(k\)个哈希值(\({h}_1, {h}_2, {h}_3, ... {h}_k\)),并依次与容器长度取余\(pos={h}_1\%w\),并将对应位置置为1,即\(A_{pos}=1\)。
判断元素是否存在时,也是类似,当想判断\(x\)值,对\(x\)做\(k\)次哈希,得到\(k\)个哈希值(\({h}_1, {h}_2, {h}_3, ... {h}_k\)),并依次与容器长度取余 \(pos={h}_1\%w\),若计算所得位置上皆为1,即\(A_{pos}==1\),则说明该元素可能存在容器中,否则可能不存在。
公式
插入元素:一个长度为\(w\)的位数组\(A\),当想插入\(x\)值时,
- \(H = { f_1(x), f_2(x) ..., f_k(x) }\),\(H\)为哈希值集合,\(f_i\)为哈希函数
- \(P = H \% w\),\(P\) 为取余集合
- 对于\(P\)中每个元素\(j\),都有\(A_j=1\)
判断元素是否存在:一个长度为\(w\)的位数组\(A\),当想判断\(x\)值时,
- \(H = { f_1(x), f_2(x) ..., f_k(x) }\),\(H\)为哈希值集合,\(f_i\)为哈希函数
- \(P = H \% w\),\(P\) 为取余集合
- 当\(\forall j \in P, A_j==1\)成立,则认为\(x \in A\)
数学结论
当哈希函数个数为\(k\),数组容量为\(w\),插入数据数量为\(n\),则当
\[ k = (w/n) * \ln 2 \]
时,布隆过滤器获得最优的准确性。
另外,在哈希函数的个数取到最优时,要让错误率不超过\(\epsilon\),\(w\)至少需要是\(n\)的1.44倍。
实现
尝试使用Rust语言实现布隆过滤器。
用例: 1
2
3
4
5
6
7
8let mut bf = BloomFilter::new(10);
let b1 = Bytes::from(&b"hello"[..]);
let b2 = Bytes::from(&b"world"[..]);
bf.add(&b1);
let filter = bf.generate();
println!("{}", bf.contains(&filter, &b1)); // true
println!("{}", bf.contains(&filter, &b2)); // false
Hash
此处的hash函数为MurmurHash,一般用于检索操作,随机分布特性表现好,广泛运用于数据库。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40pub mod codec {
pub fn get_u32_little_end(arr: &[u8]) -> u32 {
((arr[0] as u32) << 0) +
((arr[1] as u32) << 8) +
((arr[2] as u32) << 16) +
((arr[3] as u32) << 24)
}
}
fn hash(data: &Bytes, seed: u32) -> u32 {
let m = 0xc6a4a793 as u32;
let r = 24 as u32;
let mut h = seed ^ (data.len() as u64 * m as u64) as u32;
let n = data.len() - data.len() % 4;
let mut i = 0;
while i < n {
h += codec::get_u32_little_end(&data[i..]) as u32;
h = (h as u64 * m as u64) as u32;
h ^= (h >> 16);
i += 4;
}
let flag = data.len() - i;
if flag == 3 {
h += (data.len() as u32) << 16;
} else if flag == 2 {
h += (data.len() as u32) << 8;
} else if flag == 1 {
h = (h as u64 + get_u32_little_end(&data[i..]) as u64) as u32;
h = (h as u64 * m as u64) as u32;
h ^= (h >> r);
}
return h
}
fn bloom_hash(data: &Bytes) -> u32 {
hash(data, 0xbc9f1d34)
}
BloomFilter
成员变量
- bits_per_key 表示平均每个key占用的位,即数学结论中的\(w/n\)
- k 表示k个哈希函数,通过数学结论中的公式计算可得
- key_hashes 用于存储key的哈希值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16struct BloomFilter {
bits_per_key: usize,
k: u8,
key_hashes: Vec<u32>,
}
impl BloomFilter {
fn new(bits_per_key: usize) -> Self {
let mut k = (bits_per_key as f64 * 0.69) as u8; // 0.69 = ln2
if k < 1 { k = 1; }
if k > 30 { k = 30; }
BloomFilter { bits_per_key, k, key_hashes: vec![] }
}
// ...
插入Key
插入Key时算一次哈希,理论上是要算k次的,但其实可以通过对一个哈希值进行位移来得到下一个哈希值,提高效率。 1
2
3fn add(&mut self, key: &Bytes) {
self.key_hashes.push(bloom_hash(key))
}
生成Filter
这里的写法有点特别,首先我们用字节数组替代我们认知中的位数组,比如一个长度为72的char类型数组,可以用长度为9的uint8类型数组替代。另外,可以通过对一个哈希值进行位移来得到下一个哈希值,提高效率。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33fn generate(&mut self) -> Bytes {
let mut n_bits = (self.key_hashes.len() * self.bits_per_key) as u32;
if n_bits < 64 {
n_bits = 64;
}
// 向上取整
let n_bytes = (n_bits + 7) / 8;
n_bits = n_bytes * 8;
let mut dest = BytesMut::new();
// 初始化n_bytes大小的数组,每个元素是一个u8
// 这里用字节数组表示位数组
dest.resize(n_bytes as usize + 1, 0);
// 最后一个位置存哈希值的数量
dest[n_bytes as usize] = self.k;
for v in &self.key_hashes {
let mut kh = v.clone();
// 哈希值的位移量
let delta = (kh >> 17) | (kh << 15);
for _ in 0..self.k {
let bitpos = (kh % n_bits) as usize;
dest[bitpos/8] |= (1 << (bitpos % 8));
// 通过位移来得到另一个哈希值,而不是继续用哈希函数计算
kh = (kh as u64 + delta as u64) as u32;
}
}
self.key_hashes.clear();
dest.freeze()
}
判断是否存在
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27fn contains(&self, filter: &Bytes, key: &Bytes) -> bool {
let n_bytes = filter.len() - 1;
if n_bytes < 1 {
return false
}
let n_bits = (n_bytes * 8) as u32;
// 通过最后一个位置拿到哈希值的数量
let k = filter[n_bytes];
if k > 30 {
return true
}
let mut kh = bloom_hash(key);
let delta = (kh >> 17) | (kh << 15);
for _ in 0..k {
let bitpos = (kh % n_bits) as usize;
// 如果filter对应位不是1就认为不存在
if filter[bitpos/8] as u32 & (1 << (bitpos % 8)) == 0 {
return false
}
kh = (kh as u64 + delta as u64) as u32;
}
return true
}
测试
测试分为两个指标,一个是集合存该元素在而过滤器判断为存在,另一个是集合不存在该元素而过滤器判断为存在。而第二个指标则称之为假阳性(False positive)。在\(w/n\)为10时,向过滤器插入1万个key,第一个指标是要求100%判断正确,对于第二个指标,让过滤器判断1万个不存在的key,判断错误的几率即为假阳性率。假阳性率不超过万分之二为可接受范围。

Comments