AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. I will try to implement it and log in this article. You can find the source code in here.
Node
Evey Node have five member properties. balFactor_ is the balance factor that equal to -1, 0, 1 representing the left sub-tree 1 layer taller than right sub-tree, tall equally and converse, respectively. 1
2
3
4
5
6
7
8
9template <typename T>
struct AVLNode {
typedef AVLNode<T>* NodePtr;
T value_;
NodePtr parent_;
NodePtr left_;
NodePtr right_;
signed char balFactor_;
Iterator
function increment() find the last node that is larger than current node, corresponding operator++. function decrement() find the last node that is smaller than current node, corresponding operator--. 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65template <typename T>
struct AVLTreeIterator {
// ...
typedef AVLTreeIterator<T> Self;
typedef AVLNode<T>* NodePtr;
NodePtr node_;
explicit AVLTreeIterator(NodePtr x): node_(x) {}
reference operator*() const {
return node_->value_;
}
pointer operator->() const {
return &(operator*());
}
void increment() {
if(node_->right_ != 0) {
node_ = node_->right_;
while(node_->left_ != 0) {
node_ = node_->left_;
}
} else {
NodePtr y = node_->parent_;
while (node_ == y->right_) {
node_ = y;
y = y->parent_;
}
if(node_->right_ != y) {
node_ = y;
}
}
}
void decrement() {
if(node_->parent_->parent_ == node_ && node_->balFactor_ == -2) { // end() node
node_ = node_->right_;
} else if (node_->left_ != 0) {
NodePtr y = node_->left_;
while (y->right_ != 0){
y = y->right_;
}
node_ = y;
} else {
NodePtr y = node_->parent_;
while (node_ == y->left_) {
node_ = y;
y = y->parent_;
}
node_ = y;
}
}
Self& operator++() {
increment();
return *this;
}
Self& operator--() {
decrement();
return *this;
}
// ...
Tree Property
header
Let us see a tree without value node, and the only node called header.
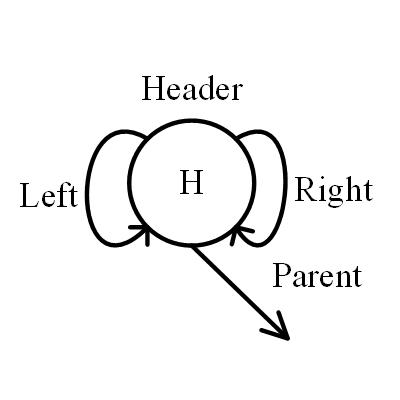
- parent: link to root if exist
- left: also call leftmost, link to the most left node of tree
- right: also call leftmost, link to the most right node of tree
- balFactor: always equal to -2 (special)
root
root is the top node of a tree.
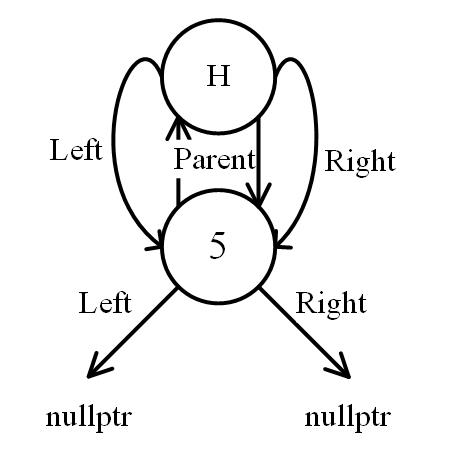
- parent: link to header
- left: link to nullptr if no node
- right: link to nullptr if no node
1
NodePtr& root() const { return header_->parent_; }
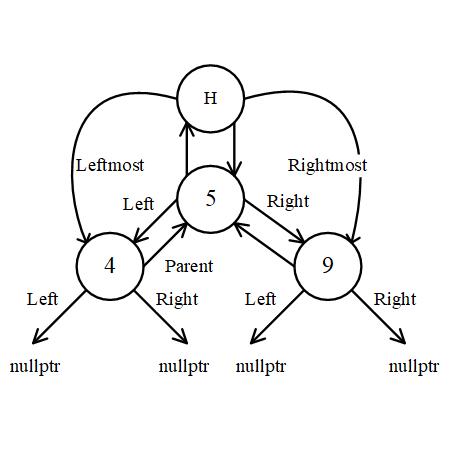
Multi Node
See a tree with three nodes. The children of leaf are nullptr.
Balance
AVL Tree (Adelson-Velskii-Landis tree) is a kind of balanced binary search tree with the demand that the difference heigth of the left and right tree cannot over 1.
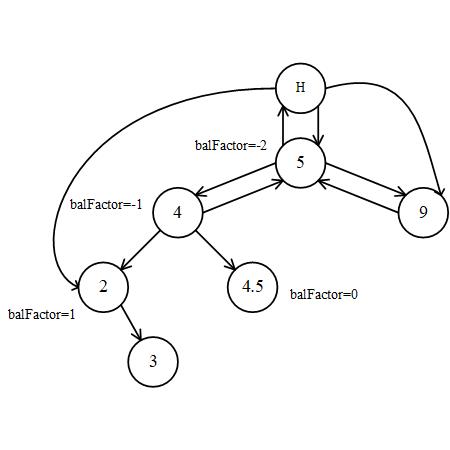
the sub-tree or tree with a root node whose balance factor = -2 or = 2 is an unbalance tree. We can rebalance it by rotation.
Rotation
Left Rotation
When the right sub-tree is taller, we need to rotate left to shorten it. 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59/*
* / /
* x y
* / \ / \
* a y => x c
* / \ / \
* [b] c a [b]
*/
void _rotateLeft(NodePtr x, NodePtr &root) {
NodePtr y = x->right_;
// change the child
x->right_ = y->left_;
y->left_ = x;
// change the parent
y->parent_ = x->parent_;
x->parent_ = y;
if(x->right_ != nullptr) { // b
x->right_->parent_ = x;
}
if(x == root) {
root = y;
} else if(y->parent_->right_ == x) { // x is the right son of his parent
y->parent_->right_ = y;
} else {
y->parent_->left_ = y;
}
if(y->balFactor_ == 1) {
/*
* / /
* x y
* / \ / \
* a y => x c
* / \ / \ /
* b c a b d
* /
* d
*/
y->balFactor_ = 0;
x->balFactor_ = 0;
} else {
/*
* / /
* x y
* / \ / \
* a y => x c
* / \ / \
* b c a b
* \ \
* d d
*/
y->balFactor_ = -1;
x->balFactor_ = 1;
}
}
Right Rotation
When the left sub-tree is taller, we need to rotate right to shorten it. 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36/*
* / /
* x y
* / \ => / \
* y a c x
* / \ / \
* c [b] [b] a
*/
void _rotateRight(NodePtr x, NodePtr &root) {
NodePtr y = x->left_;
x->left_ = y->right_;
y->right_ = x;
y->parent_ = x->parent_;
x->parent_ = y;
if(x->left_ != nullptr) { // b
x->left_->parent_ = x;
}
if(x == root) {
root = y;
} else if(y->parent_->right_ == x) {
y->parent_->right_ = y;
} else {
y->parent_->left_ = y;
}
if(y->balFactor_ == -1) {
y->balFactor_ = 0;
x->balFactor_ = 0;
} else {
y->balFactor_ = 1;
x->balFactor_ = -1;
}
}
Left Right Rotation
As for Double rotation, we need to look four layers of tree. When the top node of tree or sub-tree has 2 layers taller left sub-tree, and the left sub-tree have a taller right sub-tree,
- we need to do a left rotation to make the latter right sub-tree shorter firstly
- and then do a right rotation to make the former left sub-tree shorter shorter secondly
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71/*
* / /
* a c
* / \ / \
* b g => / \
* / \ b a
* d c / \ / \
* / \ d e f g
* e f
*/
void _rotateLeftRight(NodePtr a, NodePtr &root) {
NodePtr b = a->left_;
NodePtr c = b->right_;
// a and b link to c' sons
a->left_ = c->right_;
b->right_ = c->left_;
// c becomes the parent of a and b
c->right_ = a;
c->left_ = b;
// c links to the parent of a and b
c->parent_ = a->parent_;
a->parent_ = b->parent_ = c;
// check c' sons and link to their new parent
if(a->left_) { // f
a->left_->parent_ = a;
}
if(b->right_) { // e
b->right_->parent_ = b;
}
// the parent of a and b link to c
if(a == root) {
root = c;
} else if(c->parent_->left_ == a) {
c->parent_->left_ = c;
} else {
c->parent_->right_ = c;
}
switch (c->balFactor_) {
case -1:
/*
* c
* /
* e
*/
a->balFactor_ = 1;
b->balFactor_ = 0;
break;
case 0:
a->balFactor_ = 0;
b->balFactor_ = 0;
break;
case 1:
/*
* c
* \
* f
*/
a->balFactor_ = 0;
b->balFactor_ = -1;
break;
default:
assert(false);
}
c->balFactor_ = 0;
}
Right Left Rotation
As for Double rotation, we need to look four layers of tree. When the top node of tree or sub-tree has 2 layers taller right sub-tree, and the right sub-tree have a taller left sub-tree,
- we need to do a right rotation to make the latter left sub-tree shorter firstly
- and then do a left rotation to make the former right sub-tree shorter shorter secondly.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66/*
* / /
* a c
* / \ / \
* d b => / \
* / \ a b
* c g / \ / \
* / \ d e f g
* e f
*/
void _rotateRightLeft(NodePtr a, NodePtr &root) {
NodePtr b = a->right_;
NodePtr c = b->left_;
a->right_ = c->left_;
b->left_ = c->right_;
c->left_ = a;
c->right_ = b;
c->parent_ = a->parent_;
a->parent_ = b->parent_ = c;
if(a->right_) {
a->right_->parent_ = a;
}
if(b->left_) {
b->left_->parent_ = b;
}
if(a == root) {
root = c;
} else if(c->parent_->left_ == a) {
c->parent_->left_ = c;
} else {
c->parent_->right_ = c;
}
switch(c->balFactor_) {
case -1:
/*
* c
* /
* e
*/
a->balFactor_ = 0;
b->balFactor_ = 1;
break;
case 0:
a->balFactor_ = 0;
b->balFactor_ = 0;
break;
case 1:
/*
* c
* \
* f
*/
a->balFactor_ = -1;
b->balFactor_ = 0;
break;
default:
assert(false);
}
c->balFactor_ = 0;
}
Insertion
When we insert a node to tree, we consider three section:
- Ensuring insert to the child of the leaf
- Considering the parent of new node is header, means that the new node is root, and that we need to add the relation between header and root, including the parent of them each other and the leftmost or rightmost.
- Rebalance. We consider the parent of x at the start, and percolate up the path from leaf to root. We at least do zero or once rotation for certein.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75// [x] is the new node to insert
// [p] is the parent of [x]
void _insertAndRebalance(bool insertLeft, NodePtr x, NodePtr p) {
// construct the new node to insert
x->parent_ = p;
x->left_ = nullptr;
x->right_ = nullptr;
x->balFactor_ = 0;
if(insertLeft) {
p->left_ = x;
if(p == header_) { // consider that p is header
header_->parent_ = x;
header_->right_ = x;
} else if(p == header_->left_) { // consider that p is son of header
header_->left_ = x;
}
} else {
p->right_ = x;
if(p == header_->right_) {
header_->right_ = x;
}
}
// rebalance
while(x != root()) {
switch (x->parent_->balFactor_) {
case 0:
// same tall right and left sub tree of x parent.
// One of them will become taller after insert a node.
x->parent_->balFactor_ = (x == x->parent_->left_) ? -1 : 1;
x = x->parent_; // percolate up the path
break;
case 1:
// right sub-tree is taller
if(x == x->parent_->left_) {
// If inserted node in the left, become same tall.
x->parent_->balFactor_ = 0;
} else {
// If inserted node in the right, become more taller probably.
// For shortening it, we need to rotate it.
if(x->balFactor_ == -1) {
// x have a taller left, do a right left rotation to shorten the left
_rotateRightLeft(x->parent_, root());
} else {
// just do a left rotation to shorten the right.
_rotateLeft(x->parent_, root());
}
}
// adjust once is enough
return;
case -1:
// -1 mean that x parent have a taller sub-left tree
if(x == x->parent_->left_) {
// but insert a new node in sub-left tree
// leading to become more taller (probably)
// For shortening it, we need to rotate it.
if(x->balFactor_ == 1) {
// If x have a taller sub-right tree,
// doing a left right rotation can shorten the right.
_rotateLeftRight(x->parent_, root());
} else {
// Else, just do a right rotation to shorten the left.
_rotateRight(x->parent_, root());
}
} else {
x->parent_->balFactor_ = 0;
}
return;
default:
assert(false);
}
}
}
We insert a not-allow-replaced key with three considerations:
- insert to the left of leftmost
- insert to the right of y if just bigger than y
- insert to the left of y if just bigger than decrement(y)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36pair<iterator, bool> insertUnique(const Val& v) {
NodePtr x = root();
NodePtr y = header_;
bool comp = true;
while(x != nullptr) {
y = x;
comp = keyComp_(KeyOfValue()(v), key(x));
x = comp ? left(x) : right(x);
}
iterator j = iterator(y);
if(comp) { // left
if(j == begin()) { // leftmost
return pair<iterator, bool>(_insert(x, y, v), true);
} else {
--j;
}
}
if(keyComp_(key(j.node_), KeyOfValue()(v))) {
return pair<iterator, bool>(_insert(x, y, v), true);
}
return pair<iterator, bool>(j, false);
}
// [x] is the child of [p],
// always is nullptr passed from insertUnique() and insertEqual(),
// do not need to consider, in theory.
// [p] is the parent of [x]
iterator _insert(NodePtr x, NodePtr p, const Val& v) {
bool insertLeft = (x != nullptr ||
p == header_ || keyComp_(KeyOfValue()(v), key(p)));
NodePtr z = createNode(v);
_insertAndRebalance(insertLeft, z, p);
++nodeCount_;
return iterator(z);
}
Insertion of allowing equal key. 1
2
3
4
5
6
7
8
9iterator insertEqual(const Val& v) {
NodePtr x = root();
NodePtr y = header_;
while(x != nullptr) {
y = x;
x = keyComp_(KeyOfValue()(v), key(x)) ? left(x) : right(x);
}
return _insert(x, y, v);
}
Deletion
When we delete a node from a tree, we consider three sections:
- Find the successor to replace the position of deleted node.
- If the node to be deleting has only one child, the successor is the child.
- If it has two children, the successor is the last node that is larger than it.
- The replacement action including three steps:
- Disconnecting to its children and make the successor links to them
- Suturing the wound caused by successor moved
- Its parent link to the successor
- Rebalance. We will percolate up and rotate multi times probably until
- the balFactor of certain node is 0, we just change its balFactor to -1 or 1 (depending the deleted node in right or left).
- the balFactor of certain node after rotation becomes from 1 to -1 or from -1 to 1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132// erase node [z] and return the deleted node
NodePtr _eraseAndRebalance(NodePtr z) {
NodePtr y = z;
NodePtr x = nullptr;
NodePtr xParent = nullptr;
// x is the child of y
if(y->left_ == nullptr) {
x = y->right_;
} else if(y->right_ == nullptr) {
x = y->left_;
} else {
// y has two children
// find the successor
y = y->right_;
while(y->left_) {
y = y->left_;
}
x = y->right_; //y has no left child, so x is the successor
}
if(y != z) { // mean that z has two children
// we make the successor y to replace z
// z will disconnect to its children and y link to them
z->left_->parent_ = y;
y->left_ = z->left_;
if(y != z->right_) {
// y will be moved, need to link its child to its parent
xParent = y->parent_;
if(x) {
x->parent_ = y->parent_;
}
y->parent_->left_ = x;
y->right_ = z->right_;
z->right_->parent_ = y;
} else {
// y == z->right, mean y has no left child and x is the right of y
xParent = y;
}
// link z's parent to y
if(root() == z) {
root() = y;
} else if(z->parent_->left_ == z) {
z->parent_->left_ = y;
} else {
z->parent_->right_ = y;
}
y->parent_ = z->parent_;
y->balFactor_ = z->balFactor_;
} else { // mean that z has one child or none and y == z
// x become the successor
xParent = y->parent_;
if(x) {
x->parent_ = y->parent_;
}
if(root() == z) {
root() = x;
} else if (z->parent_->left_ == z) {
z->parent_->left_ = x;
} else {
z->parent_->right_ = x;
}
if(leftmost() == z) {
if(z->right_ == nullptr) {
leftmost() = z->parent_;
} else {
leftmost() = Node::minimum(x);
}
}
if(rightmost() == z) {
if(z->left_ == nullptr) {
rightmost() = z->parent_;
} else {
rightmost() = Node::maximum(x);
}
}
}
// rebalance
while (x != root()) {
switch (xParent->balFactor_) {
case 0:
xParent->balFactor_ = (x == xParent->right_) ? -1 : 1;
return z;
case -1:
// left sub-tree taller
if(x == xParent->left_) { // erase the node in the left, balance just right
xParent->balFactor_ = 0;
x = xParent;
xParent = xParent->parent_;
} else { // erase the node in the right, need to shorten the left
NodePtr a = xParent->left_;
if(a->balFactor_ == 1) { // check whether need a double rotation
_rotateLeftRight(a, root());
} else {
_rotateRight(xParent, root());
}
// percolate up
x = xParent->parent_;
xParent = xParent->parent_->parent_;
if(x->balFactor_ == 1) {
return z;
}
}
break;
case 1:
// right sub-tree taller
if(x == xParent->right_) {
xParent->balFactor_ = 0;
x = xParent;
xParent = xParent->parent_;
} else {
NodePtr a = xParent->right_;
if(a->balFactor_ == -1) {
_rotateRightLeft(a, root());
} else {
_rotateLeft(xParent, root());
}
x = xParent->parent_;
xParent = xParent->parent_->parent_;
if(x->balFactor_ == -1) {
return z;
}
}
break;
default:
assert(false);
}
}
return z;
}
Nothing additional thing If need to delete a known node. 1
2
3
4
5void erase(iterator pos) {
NodePtr y = _eraseAndRebalance(pos.node_);
destroyNode(y);
--nodeCount_;
}
Deleting a key that probably exists in multi node, we need to find the range and delete them one by one.
lowerBound() can find the last node that greater than or equal to a certein key. And upperBound() find the last node that greater than a certein key. So the deleted range is [lowerBound(), upperBound()). 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48size_type erase(const Key& k) {
pair<iterator, iterator> p = equalRange(k);
size_type old = size();
erase(p.first, p.second);
return old - size();
}
void erase(iterator first, iterator last) {
if(first == begin() && last == end()) {
clear();
} else {
while (first != last) {
erase(first++);
}
}
}
pair<iterator, iterator> equalRange(const Key& k) const {
return pair<iterator, iterator>(lowerBound(k), upperBound(k));
}
iterator lowerBound(const Key& k) const {
NodePtr y = header_;
NodePtr x = root();
while(x != nullptr) {
if(!keyComp_(key(x), k)) {
y = x;
x = left(x);
} else {
x = right(x);
}
}
return iterator(y);
}
iterator upperBound(const Key& k) const {
NodePtr y = header_;
NodePtr x = root();
while(x != nullptr) {
if(keyComp_(k, key(x))) {
y = x;
x = left(x);
} else {
x = right(x);
}
}
return iterator(y);
}
Find
Using lowerBound, we can find the last node that greater than or equal to a certein key, if no, return the header node. And we only need the node with the same key. 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20iterator lowerBound(const Key& k) const {
NodePtr y = header_;
NodePtr x = root();
while(x != nullptr) {
if(!keyComp_(key(x), k)) {
y = x;
x = left(x);
} else {
x = right(x);
}
}
return iterator(y);
}
iterator find(const Key& k) {
iterator j = lowerBound(k);
// 1. j will be end() if cannot find
// 2. key(j) probably less than k
return (j == end() || keyComp_(k, key(j.node_))) ? end() : j;
}

Comments